3945: 蓝桥杯C++真题(13):最大值
Description
题目描述:
手工课上老师拿出N张长方形彩纸,且每张彩纸上都画着W * H的网格(网格铺满整张彩纸)。现在老师将N张彩纸裁剪出K张大小相同的正方形,并且要使裁剪出的正方形的边长最大(裁剪的正方形边长必须为整数)。
例如:N=2, 有2张彩纸,第一张彩纸W = 4, H = 3:第二张彩纸W = 5,H = 4; K = 6,裁剪的6个正方形边长最大是2。
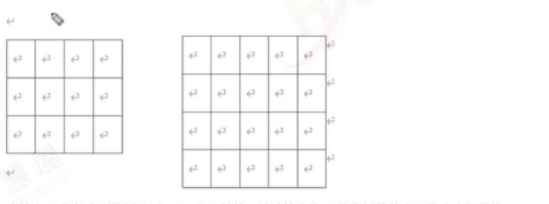
当给出N张长方形彩纸W和H,及K的值,请青计算出将N张彩纸裁剪出K张大小相同的正方形,正方形的边长最大是多少(裁剪的正方形边长必须为整数)。
Input
第一行输入两个正整数N,K(1<N<100,1<K<100), N表示彩纸数量,K表示需裁剪的正方形数量,两个正整数之间一个空格隔开.
第二行开始,输入N行,每行输入两个正整数Wi,Hi (1 < Wi < 1000,1 < Hi < 1000,且 Wi≠Hi,,Wi表示彩纸的长度,Hi表示彩纸的宽度,两个正整数之间一个空格隔开.
Output
输出一个正整数,表示将N张彩纸裁剪出K张大小相同的正方形的边长最大是多少(裁剪的正方形边长必须为整数),如果不能裁剪出K张正方形就输出“-1”
Sample Input Copy
2 6
4 3
5 4Sample Output Copy
2HINT
题目要求将N张彩纸裁剪出K张大小相同的正方形,并且要使裁剪出的正方形的边长最大,裁剪的正方形边长必须为整数。
因为要裁剪的正方形大小是一样的,所以可以把所有彩纸的网格拼接在一起,然后对整个网格进行切割,最终得到的正方形大小就是所有裁剪出的正方形的大小。而要求裁剪出的正方形的边长最大,也就是要求最终得到的正方形大小最大。
因此,我们可以采用二分答案的思想。设定一个边长mid,然后对整个网格进行切割,看能否得到K个大小为mid的正方形。如果可以,那么继续增大mid;如果不行,那么缩小mid。
具体实现时,可以用一个check函数来检查在给定的边长下,是否能够得到K个正方形。check函数中,可以用贪心的思想,从左上角开始切割,每次切割出一个正方形,直到切割出K个正方形或者无法再切割为止。如果能够切割出K个正方形,说明当前的mid太小,需要增大;否则,说明当前的mid太大,需要缩小。
时间复杂度:O(NWlog(S)),其中W为彩纸的最大边长,S为所有彩纸网格的总面积。