3989: 中山市第十二届义务教育段学生信息学邀请赛:六形棋（chess）

【问题描述】

Jimmy 和 Chen 在下一种奇怪的棋，叫做六形棋。

棋盘由 N × N 个六边形格子构成，如下图所示：

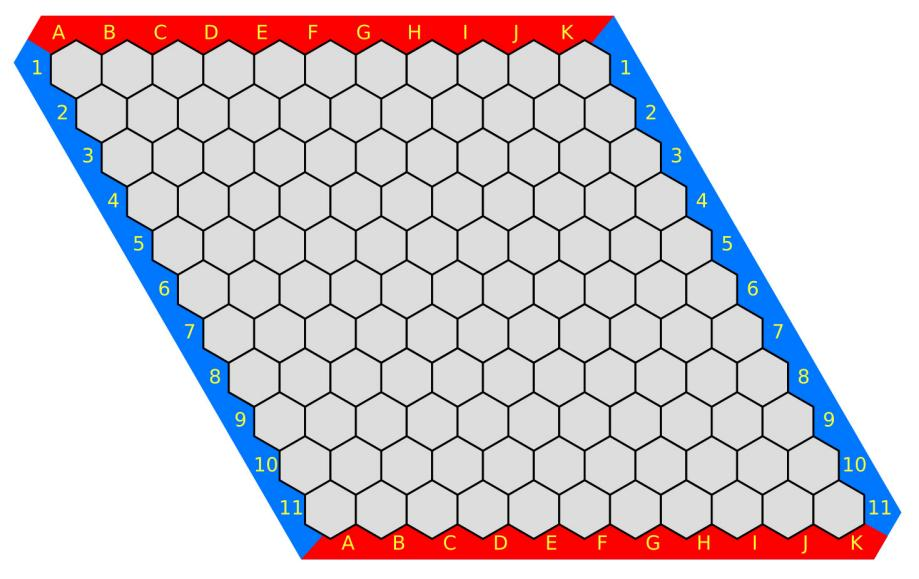
当棋盘上的两个六边形格子有一条边重合的时候， 我们称两个格子是互相连通的。将从  上往下第 i 行、从左到右第 j  个格子称为 (i, j)。对于一个不在边界上的格子 (i, j)，它和  (i, j + 1) ，(i, j − 1) ，(i + 1, j) ，(i + 1, j − 1) ，(i − 1, j) ，(i − 1, j + 1) 这 6 个格子互相连通， 而边界上的格子只与上述格子中未出界的格子互相连通。

六形棋的游戏规则如下： 两人轮流下棋， Jimmy 先手， Jimmy 每次选一个空的格子下 一个红色棋子， 接下来 Chen 每次选一个空的格子下一个蓝色棋子， 依次类推。如果最后 Jimmy 将上下两条红色的边界用红色棋子连通了， 那么 Jimmy 胜； 相反， 如果 Chen 将左 右两条蓝色边界用蓝色棋子连通了，那么 Chen 胜。

接下来给出若干个六形棋的棋盘， 请你判断每一局是 Jimmy 胜， 还是 Chen 胜， 还是 目前未分出胜负（容易证明，不可能两人都达到获胜条件）。

【输入格式】

本题输入有多组测试数据。

第一行一个正整数 T ，代表他们下了 T 盘棋。

每组数据的第一行为一个正整数 N，代表棋盘的大小。

每组数据的第 2 ∼ N + 1 行， 每行 N 个 −1, 0, 1  中的整数， 第 i + 1 行的第 j  个整数代 表格子 (i, j) 的状态， 如果为 −1 则该格子中为蓝色棋子， 如果为 0 则该格子为空， 如果为1 则该格子中为红色棋子。

本题输入有多组测试数据。

第一行一个正整数 T ，代表他们下了 T 盘棋。

每组数据的第一行为一个正整数 N，代表棋盘的大小。

每组数据的第 2 ∼ N + 1 行， 每行 N 个 −1, 0, 1  中的整数， 第 i + 1 行的第 j  个整数代 表格子 (i, j) 的状态， 如果为 −1 则该格子中为蓝色棋子， 如果为 0 则该格子为空， 如果为1 则该格子中为红色棋子。